The ultimate goal of pavement data collection is to be able to most efficiently allocate resources to plan for pavement maintenance. When it comes to programming maintenance and rehabilitation (M&R) activities, all decisions are bound by resource constraints. A typical pavement network optimization problem is trying to produce the best set of pavement projects to meet a defined set of constraints, while maximizing or minimizing some objectives. This means that the desired output of the analysis is a work plan that include the following components:
- Where: which sections to fix
- What: which treatment(s) to use or not use
- When: in which year
Usually there are some assumptions regarding this problem, such as:
- A set of pavement sections has been defined in some scope
- Based upon some defined set of rules, an appropriate treatment can be recommended for each section
- These recommended treatments depend on the section’s attributes, such as condition, functional class, and traffic level
- This set of rules often exists in the form a decision tree for many transportation agencies
Therefore, in an analysis where the analysis period is one year, the work plan will include one of the following options for each section in the defined scope:
- Treat this section using the recommended treatment
- Do not treat the section (Do Nothing)
The analysis performs this decision making on a network-wide basis and the sum of activities recommended by the analysis should optimally achieve the stated objective.
Optimization Approach
Developing a work plan is essentially an optimization problem because in real-world scenarios there are always some resource constraints that prevents applying treatments to all the sections in the network. An optimization problem can usually be formulated as follows:
- The intention is to maximize or minimize a value in what is called Objective Function
- The problem is limited by some set of rules that control how the output is manipulated by what are called Constraints
- The dynamics between the objective and constraints can be changed by varying some set of values called Variables
In general, the way to specify an optimization type problem is to state:
- I want to maximize or minimize this (Objective)
- Subject to these conditions being true (Constraint A,B,C)
- By varying these quantities (Variable X1, X2, X3 …)
Mathematical Formulation
In the context of pavement, the work plan is essentially a set of binary values, with each value corresponding to a given section at a given year, namely:
- 1 = Treat this section using the corresponding treatment
- 0 = Do nothing
Therefore, conceptually the work plan could be a list of 0’s and 1’s like this: [0,0,1,1,0,1,1,1,1,0….0]. For example, if there are 5 sections in the analysis scope, then the following are two possible work plans (Note: They may not be the optimal work plan):
- [0,0,0,1,0] - This means treating the 4th section with the recommended treatment
- [1,1,1,0,1] - This means treating every section EXCEPT the 4th section with their corresponding candidate treatments from the decision tree
Define the Variables
- These are the 0’s and 1’s that make up the work plan
- These 0’s and 1’s can be changed to find the desired solutions
- Essentially the analysis is trying different combinations of these sets of 0’s and 1’s until it settle on a combination that fits the desired solution
- All of these 0’s and 1’s can be referenced by the variable number. This manual uses the notation Xi to indicate the variable of section i. Example: X4 will be the variable for the 4th section in the list
Define the Constraints
- Constraints can be set in many ways but they are all functions of the problem variables
- Take a budget constraint as an example where the total treatment cost must be less than a given amount. If the cost of the recommended treatment for each section is ci,
- the cost for a given section is ci*xi
- the total treatment cost is
- Therefore, if the total budget allowed is C, then the constraint equation is
AgileAssets application allows the user to define a variety of other constraint types including weighted average, percent above threshold and sub-constraints.
With the mathematical formulation of the problem, it is possible to use an optimization software, or Solver, to solve the problem.
Optimize Analysis
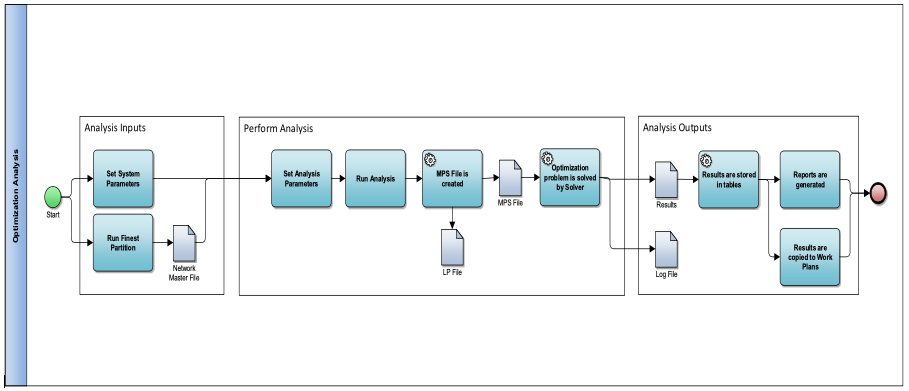
Generally, Optimization Analysis using AgileAssets framework is performed in three phases:
- Prepare analysis Inputs
- Perform analysis
- Review analysis outputs
The optimization process in Pavement Analyst looks like this: